一种简明的浮点精度介绍
一种理解浮点数精度的不同方式。
组成
一个 32 位(一般是 float )的浮点数,在内存中会被分为 3 个部分:
- 符号位(占 1 位)
- 指数(占 8 位):指定范围(range)
- 尾数(占 23 位):指定偏移(offset)
双精度(
double)则是1、11、52
表示
使用这 32 位来表示一个十进制值可以看作三步,每一个步骤分别由符号位、范围位和偏移位来处理:
- 确定值是正数还是负值;
- 定义一个范围来封装要表示的值;
- 在定义的范围内选择一个值。
第一步非常简单,如果符号位为 1 则表示的浮点数为负数;
第二步用来定义范围的指数用于定义 整数。由于有 8 位可以使用,因此该整数的范围是 0 - 255 之间的任意整数。但是,为了能表示负值,将得到值减去 127。
这样的话,表示的值的范围就是 -127 - 127,意味着如果要表示 0 ,则应该使用 127,即 0111 1111。现在,将这个整数视为 2 的幂次,例如:如果这个值是 0000 0001(即 1),那么这个浮点数可以表示的最低可能值将是 +/-,而上限则是以这个整数 +1 得到的指数。如果 是下限,那么 一定是上限。所以,这个整数意义就在于确定了 范围。
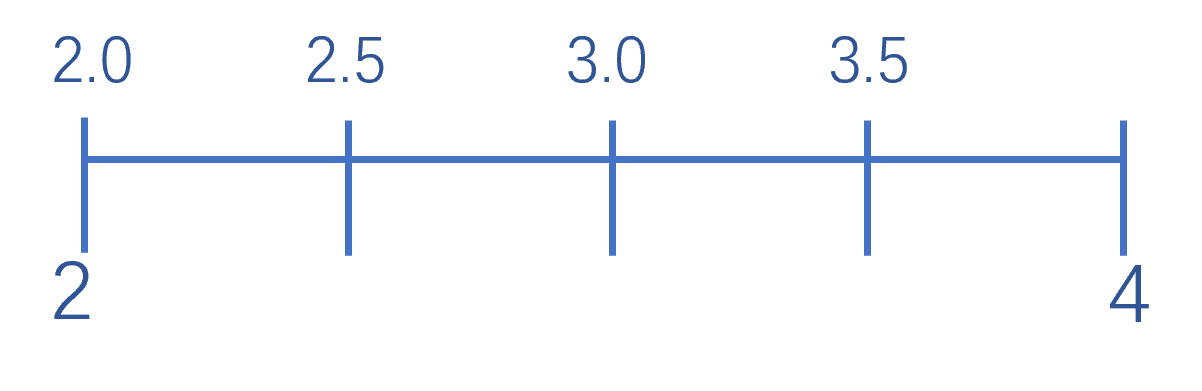
最后,就是从上一步确定的范围中选择一个值,而这就是最后 23 位的用途。为了便于理解,这里假设这部分只有 2 位,而不是 23 位,那么就只能表示 00、01、10 和 11 这四个值,也就是 0 - 3。这就意味着最终的浮点数可以表示在范围内的这 4 个值。
如果是 是下限,那么 是上限。这 4 个值均匀分布在数轴上则如下图所示:
| 值 | 计算过程 |
|---|---|
| 2 | |
| 2.5 | |
| 3.0 | |
| 3.5 |
这 4 个值是这个浮点数所能表示的值。如果试图在这种情况下保存 2.4,那么就会被「捕获」到最接近的值,即 2.5。
如果范围变大,那么这些边界就之间的值就变得不确定。这意味着随着在浮点数中存储的值增加,对它的表示就越不准确。
如果现在是 23 位,则可以表示 个值,那么前 4 个值则是,
| 值 | 计算过程 |
|---|---|
| 2 | |
| 2.000000238418579 | |
| 2.000000476837158 | |
| 2.0000007152557373 |
可以看到,仍然无法表示 2.0000003。
小结
准确来讲,上述的内容并不是特别的严谨,只是提供了一种直观理解浮点数精度的视角。建议还是参考类似《深入理解计算机系统》之类的书籍进一步深入理解。