特征点

图像本身是一个由亮度和色彩组成的矩阵，如果直接从矩阵层面考虑运动估计，将会非常困难。

所以，比较方便的做法是：首先，从图像中选取比较有代表性的点。这些点在相机视角发生少量变化后会 保持不变 ，于是我们能在各个图像中找到相同的点。

指出某两幅图像中出现同一个区块则是最困难的。我们发现，图像中的 角点 、边缘相比于像素区块而言更加「特别」。在这种做法中，角点就是所谓的特征。角点的提取算法有很多，例如：Harris 角点、FAST 角点、GFTT 角点，等等。它们大部分是 2000 年以前提出的算法。

在大多数应用中，单纯的角点依然不能满足我们的很多需求。例如，从远处看上去是角点的地方，当相机离近之后，可能就不显示为角点了。

或者，当旋转相机时，角点的外观会发生变化，我们也就不容易辨认出那是同一个角点了。

为此，计算机视觉领域的研究者们在长年的研究中设计了许多更加稳定的局部图像特征，如著名的 SIFT、SURF、ORB，等等。

特征点由 关键点 (Key-point)和 描述子 (Descriptor)两部分组成。

例如，当我们说「在一张图像中计算 SIFT 特征点」时，是指「提取 SIFT 关键点，并计算 SIFT 描述子」两件事情。

  • 关键点是指该特征点在图像里的 位置，有些特征点还具有朝向、大小等信息。
  • 描述子通常是一个 向量 ，按照某种人为设计的方式，描述了该关键点周围像素的信息。

SIFT（尺度不变特征变换，Scale-Invariant Feature Transform）当属最为经典的一种。它充分考虑了在图像变换过程中出现的光照、尺度、旋转等变化，但随之而来的是极大的计算量。

计算相机运动

  1. 当相机为单目时，我们只知道 2D 的像素坐标，因而问题是根据两组 2D 点估计运动。该问题用 对极几何 解决。
  2. 当相机为双目、RGB-D 时，或者通过某种方法得到了距离信息，那么问题就是根据两组 3D 点估计运动。该问题通常用 ICP 解决。
  3. 如果一组为 3D，一组为 2D，即，我们得到了一些 3D 点和它们在相机的投影位置，也能估计相机的运动。该问题通过 PnP 求解。

2D-2D：对极几何

对极约束

现在要求取两帧图像 I1,I2I_1,I_2 之间的运动，设从第一帧到第二帧的运动为 R,tR,t。

两个相机的中心分别为 O1,O2O_1,O_2。现在，考虑 I1I_1 中有一个特征点 p1p_1，它在 I2I_2 中对应着特征点 p2p_2。两者之间是通过特征匹配得到的。

如果匹配正确，说明它们确实是 同一个空间点在两个成像平面上的投影。

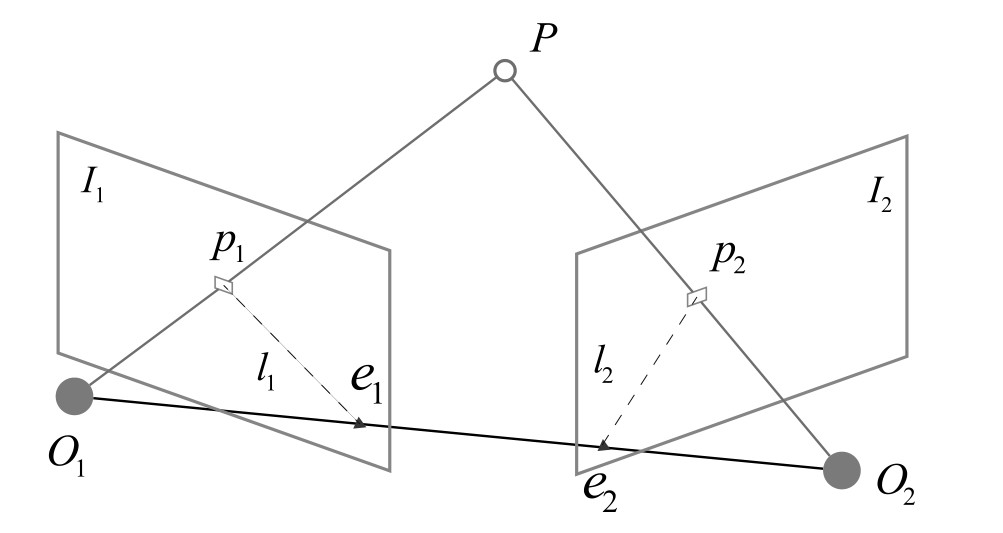
对极几何约束

  • O1,O2,PO_1,O_2,P 三个点可以确定一个平面，称为 极平面（Epipolar plane）
  • O1,O2O_1,O_2 连线与像平面 I1,I2I_1,I_2 的交点分别为 e1,e2e_1,e_2。
    • e1,e2e_1,e_2 称为 极点
    • O1O2O_1O_2 称为 基线
    • 极平面与两个像平面 I1,I2I_1,I_2 之间的相交线 l1,l2l1,l_2 为极线

O1P1→\overrightarrow{O_1P_1} 是某个像素可能出现的空间位置。在正确的特征匹配下，确定了 p2p_2 的位置，从而可以推断 PP 的位置。

设 PP 的空间位置为：

P=[X,Y,Z]TP=[X,Y,Z]^T

基于针孔相机模型，两个像素 p1p_1，p2p_2 的像素位置为：

s1p1=KP,s2p2=K(RP+t)s_1p_1=\mathbf{KP},s_2p_2=\mathbf{K}(\mathbf{RP}+t)

这里的 K\mathbf{K} 是相机内参矩阵，R,tR,t 为两个坐标系的相机运动。

s1p1s_1p_1 和 p1p_1 成投影关系，它们在齐次坐标的意义下是相等的。这种相等关系为 尺度意义下相等（equal up to a scale），记作：

sp≃psp \simeq p

那么，上述的投影关系可以写为：

p1≃KP,p2≃K(RP+t)p_1 \simeq \mathbf{KP}, p_2 \simeq \mathbf{K}(\mathbf{RP} + t)

现在，取：

x1=K−1p1,x2=K−1p2x_1=\mathbf{K}^{-1}p_1,x_2=\mathbf{K}^{-1}p_2

这里的 x1,x2x_1,x_2 是像素点的归一化平面上的坐标。代入上式，得：

x2≃Rx1+tx_2\simeq \mathbf{R}x_1 + t

同时左乘 t^，

t∧x2≃t∧Rx1t^\wedge x_2 \simeq t^\wedge \mathbf{R}x_1

然后同时左乘 x2Tx_2^T

x2Tt∧x2≃x2Tt∧Rx1x_2^T t^\wedge x_2 \simeq x_2^T t^\wedge \mathbf{R}x_1

左侧 t∧x2t^\wedge x_2 是一个与 tt 和 x2x_2 都垂直的向量。它再和 x2x_2 做内积的到时候，将得到 0。

等式左侧严格为零，乘以任意非零常数之后也为零，因此可以写成：

x2Tt∧Rx1=0x_2^T t^\wedge \mathbf{R}x_1 = 0

代入 p1,p2p_1,p_2，

p2TK−Tt∧RK−1p1=0p_{2}^{T}\mathbf{K}^{-T} t^\wedge \mathbf{RK}^{-1}p_1=0

这两个式子都称为 对极约束，以简洁著名。它的几何意义是 O1,P,O2O_1,P,O_2 三者共面，同时包含了平移和旋转。

中间的两个部分记为两个矩阵：

  • 基础矩阵（Fundamental Matrix）F\mathbf{F}
  • 本质矩阵（Essential Matrix）E\mathbf{E}

进一步简化约束，

E=t∧R,F=K−TEK−1,x2TEx1=p2TFp1\mathbf{E}=t^\wedge R,\mathbf{F}=\mathbf{K}^{-T}\mathbf{EK}^{-1}, x_2^{T}\mathbf{E}x_1=p_2^{T}\mathbf{F}p_1

对极约束简洁地给出了两个匹配点的空间位置关系，于是，相机位姿估计变为以下两步：

  1. 根据配对点的像素位置求出 E\mathbf{E} 或者 F\mathbf{F}
  2. 根据 E\mathbf{E} 或者 F\mathbf{F} 求出 R,tR,t

由于 E 和 F 只差了相机内参，SLAM 中内参通常是已知的，所以实践中往往使用本质矩阵。

本质矩阵

根据定义，本质矩阵 E=t∧RE=t^\wedge R，是一个 3×3 的矩阵，共有 9 个未知数。

可以证明，本质矩阵 E 的奇异值必定是 [σ,σ,0]T[\sigma,\sigma,0]^T，这称为 本质矩阵的内在性质。

由于平移和旋转各有三个自由度，故 t∧Rt^\wedge R 共有 6 个自由度，但由于尺度等价性，E 实际上只有 5 个自由度。

E 具有 5 个自由度的事实，表明我们最少可以用 5 对点来求解 E。但是，E 的内在性质是非线性性质，估计起来会带来麻烦。

因此，也可以只考虑它的尺度等价性，使用 8 对点来估计 E，这就是经典的 八点法（Eight-point-algorithm）。

单应矩阵

二视图几何中还存在另一种常见的矩阵：单应矩阵(Homography)H，它描述了两个平面之间的映射关系。

场景中的特征点都落在同一平面上（比如墙、地面等），则可以通过单应性进行运动估计。

单应矩阵通常描述处于共同平面上的一些点在两张图像之间的变换关系。设图像 I1I_1 和 I2I_2 有一对匹配好的特征点 p1p_1 和 p2p_2。这个特征点落在平面 PP 上，设这个平面满足方程：

nTP+d=0n^T\mathbf{P} + d = 0

整理，得：

−nTPd=1-\frac{n^T\mathbf{P}}{d}=1

然后，得：

p2≃K(RP+t)≃K(RP+t⋅(−nTPd))\begin{align*} p_2 &\simeq \mathbf{K}(\mathbf{RP} + t)\\ &\simeq \mathbf{K}(\mathbf{RP} + t\cdot(-\frac{n^T\mathbf{P}}{d})) \end{align*}

于是，我们得到了一个直接描述图像坐标 p1p_1 和 p2p_2 之间的变换，把中间部分记为 HH，于是：

p2≃Hp1p_2\simeq \mathbf{H}p_1

单应性在 SLAM 中具有重要意义。当特征点共面或者相机发生纯旋转时，基础矩阵的自由度下降，这就出现了所谓的退化(degenerate)。

现实中的数据总包含一些噪声，这时如果继续使用八点法求解基础矩阵，基础矩阵多余出来的自由度将会主要由噪声决定。

参考资料

  1. 高翔等著. 视觉 SLAM 十四讲：从理论到实践（第 2 版）.2019.8
  2. OpenCV. Epipolar Geometry
  3. HZepipolar.pdf