相机投影矩阵与内外参计算 | 小谷的编程随笔空间

相机标定的目的在于为世界坐标系的三维物体和图像坐标系中的二维像素点之间建立一种映射关系。对于常规的相机标定，通常会使用棋盘格进行张氏标定，从而获得相机内参。但如果是投影机，虽然它可以视为相机模型，但是可能就没有办法直接使用棋盘格进行标定。

如果要重建投影，工业上我们考虑使用激光测距，加上屏幕投影标记点，获得世界坐标和像素坐标的映射，从而将这个问题转换为计算机视觉中经典的 PnP（Perspective-n-Point）问题。

与 OpenCV 中的 API 不同，我们并没有内参。

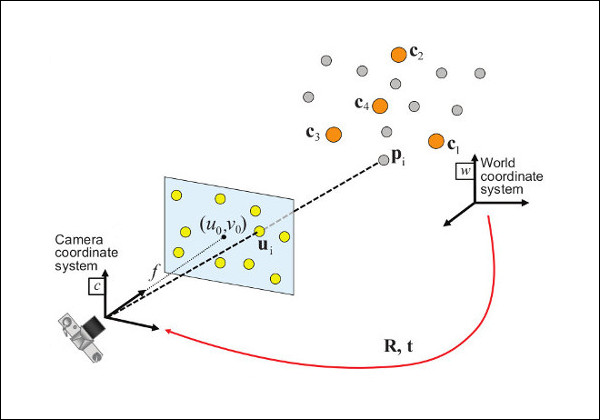
pnp model

相机模型

相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程能够用一个几何模型进行描述。这个模型有很多种，其中最简单的称为 针孔模型。

针孔模型

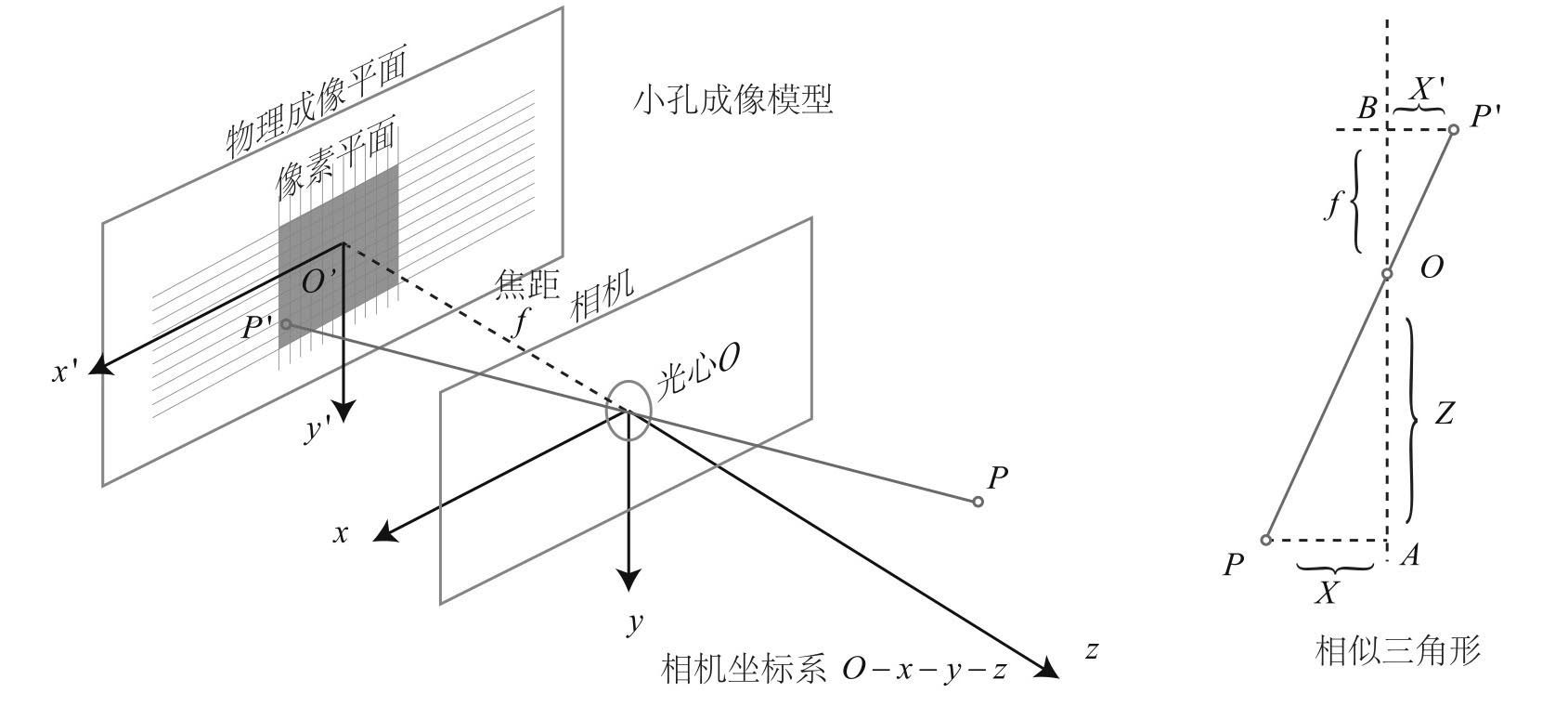
O-x-y-z 相机坐标系
- z 指向相机前方、x 轴向右、y 轴向下（右手系）
- O 是光心
空间点 P，经过小孔 O 投影到 P’
设物理成像平面到小孔的距离为 f（焦距）

根据相似三角形,

$\frac{Z}{f}=-\frac{X}{X^\prime}=-\frac{Y}{Y^\prime}$

负号表示成像是倒立的。由于可以将成像面平面对称地放到相机前方，和三维空间点在坐标系地同一侧。这样可以把负号去掉：

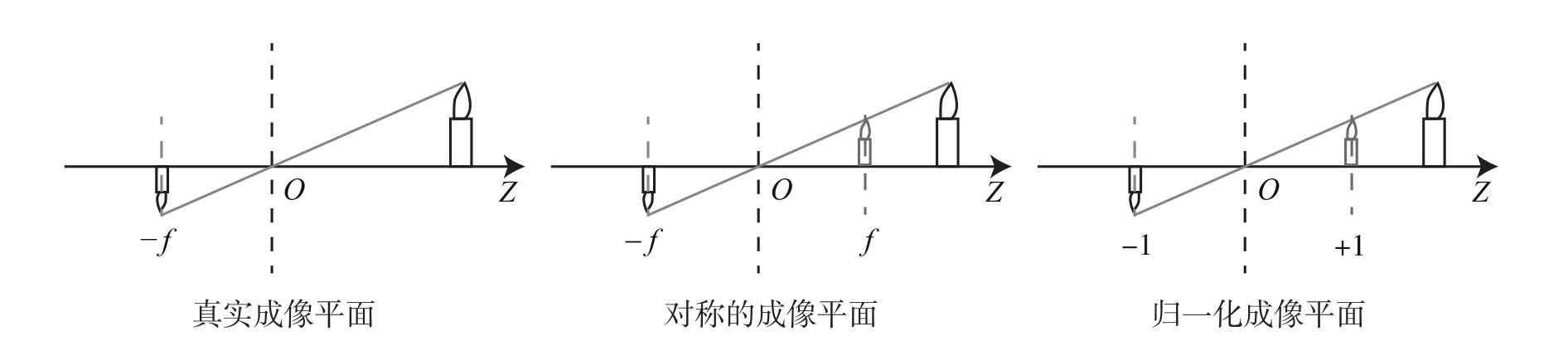
等价的针孔模型

$\frac{Z}{f}=\frac{X}{X^\prime}=\frac{Y}{Y^\prime}$

整理得到，

$\begin{align*} X^{\prime}=f\frac{X}{Z} \\ Y^{\prime}=f\frac{Y}{Z} \end{align*}$

这里描述的是空间关系，单位是米。但是我们最终需要获得一个个像素，还需要在平面上对成像进行采样和量化。换言之，我们需要将它再变换到像素坐标系。

像素坐标系 通常的定义方式是：原点 $o^\prime$ 位于图像的左上角，u 轴向右与 x 轴平行，v 轴向下与 y 轴平行。

像素坐标系和成像平面之间，相差了一个缩放和一个原点的平移。

设像素坐标在 u 轴上缩放了 $\alpha$ ，在 v 轴缩放了一个 $\beta$ 倍。同时，原点平移了 $[c_x,c_y]^T$ 。

那么， $P^{\prime}$ 的坐标与像素坐标 $[u,v]^T$ 的关系为：

$\begin{align*} u&=\alpha X^{\prime} + c_x \\ v&=\beta Y^{\prime} + c_y \end{align*}$

将 $\alpha f$ 合并为 $f_x$ ，将 $\beta f$ 合并为 $f_y$ ，得到：

$\begin{align*} u&=f_x \frac{X}{Z} + c_x \\ v&=f_y \frac{Y}{Z} + c_y \end{align*}$

其中，f 的单位是 m， $\alpha$ 、 $\beta$ 的单位是像素/米。所以 $f_x$ 、 $f_y$ 和 $c_x$ 、 $c_y$ 的单位是像素。

用矩阵形式表达会更加简洁：

$\left( \begin{matrix} u \\ v \\ 1 \end{matrix} \right) = \frac{1}{Z} \left( \begin{matrix} f_x & 0 & c_x \\ 0 & f_x & c_y \\ 0 & 0 & 1 \end{matrix} \right)\left( \begin{matrix} X \\ Y \\ Z \end{matrix} \right) \overset{def}{=}\textbf{K}\textbf{P}$

我们把中间的量组成的矩阵称为相机的 内参数 (Camera Intrinsics）矩阵 K。

相机的内参在出厂之后是固定的，不会在使用过程中发生变化。有的相机生产厂商会告诉你相机的内参，而有时需要你自己确定相机的内参，也就是所谓的标定。

由于实际中，相机有自己位姿，不可能刚好是相机坐标系原点且旋转为 0。所以我们需要先变换到相机坐标系。

相机的位姿由旋转矩阵 R 和平移向量 t 描述，那么就有：

$Z\textbf{P}_{uv} = Z\left[\begin{matrix} u \\ v \\ 1 \end{matrix}\right] =\textbf{K}(\textbf{R}\textbf{P}_w + t)=\textbf{K}\textbf{T}\textbf{P}_w$

投影过程还可以从另一个角度来看。我们可以把一个世界坐标点先转换到相机坐标系，再除掉它最后一维的数值（即该点距离相机成像平面的深度），这相当于把最后一维进行 归一化 处理，得到点 P 在相机归一化平面上的投影。

直接线性变换（DLT）

考虑某个空间点 P，它的齐次坐标为 $P=(X,Y,Z,1)^T$ 。在图像中，投影到特征点 $x_1=(u_1,v_1,1)^T$ （以归一化平面齐次坐标表示）。

此时，相机的位姿 R,t 是未知的。我们定义增广矩阵 [R|t]为一个 3×4 的矩阵，包含了旋转与平移信息。

展开形式如下：

$s\left(\begin{matrix}u_1 \\ v_1 \\ 1\end{matrix}\right) = \left( \begin{matrix} t_1 & t_2 & t_3 & t_4 \\ t_5 & t_6 & t_7 & t_8 \\ t_9 & t_{10} & t_{11} & t_{12} \end{matrix} \right) \left( \begin{matrix} X\\ Y\\ Z\\ 1 \end{matrix} \right)$

用最后一行把 s 消掉，得到两个约束

$u_1=\frac{t_1X+t_2Y+t_3Z+t_4}{t_9X+t_{10}Y+t_{11}Z+t_{12}}, v_1=\frac{t_5X+t_6Y+t_7Z+t_8}{t_9X+t_{10}Y+t_{11}Z+t_{12}}$

为了简化表达，定义行向量：

$\textbf{t}_1=(t_1,t_2,t_3,t_4),\textbf{t}_2=(t_5,t_6,t_7,t_8),\textbf{t}_3=(t_9,t_{10},t_{11},t_{12})$

于是可以将两个约束表示成：

$\textbf{t}_1 \textbf{P}-\textbf{t}_3 \textbf{P}_{u_1}=0$

和

$\textbf{t}_2 \textbf{P}-\textbf{t}_3 \textbf{P}_{v_1}=0$

请注意，t 是待求的变量，可以看到，每个特征点提供了两个关于 t 的线性约束。

列出线性方程组：

$\left( \begin{matrix} \textbf{P}_1 & 0 & -u_1\textbf{P}_1 \\ 0 & \textbf{P}_1 & -v_1\textbf{P}_1 \\ \vdots & \vdots & \vdots \\ \textbf{P}_n & 0 & -u_n\textbf{P}_n \\ 0 & \textbf{P}_n & -v_n\textbf{P}_n \end{matrix} \right) \left( \begin{matrix} \textbf{t}_1\\ \textbf{t}_2\\ \textbf{t}_3 \end{matrix} \right) =0$

t 一共有 12 维，因此最少通过 6 对匹配点即可实现矩阵 T 的线性求解 ，这种方法称为 DLT。当匹配点大于 6 对时，也可以使用 SVD 等方法对超定方程求最小二乘解。

在 DLT 求解中，我们直接将 T 矩阵看成了 12 个未知数，忽略了它们之间的联系，因此得出的矩阵只是一个一般矩阵，不一定满足约束。对于旋转矩阵 R，我们必须针对 DLT 估计的 T 左边 3×3 的矩阵块，寻找一个最好的旋转矩阵对它进行近似，所以可以使用 RQ 分解获得一个近似。

import numpy as np

def estimate_camera_matrix(points3D, points2D):
    assert len(points3D) == len(points2D), "Number of 3D and 2D points should be the same"
    
    # 将3D点和2D点转换为齐次坐标
    pts3D_hmg = np.hstack((points3D, np.ones((len(points3D), 1))))
    pts2D_hmg = np.hstack((points2D, np.ones((len(points2D), 1))))
    
    # 构造矩阵A
    A = np.zeros((2 * len(points3D), 12))
    for i in range(len(points3D)):
        A[2*i, 4:8] = -pts3D_hmg[i]
        A[2*i, 8:12] = pts2D_hmg[i, 1] * pts3D_hmg[i]
        A[2*i+1, 0:4] = pts3D_hmg[i]
        A[2*i+1, 8:12] = -pts2D_hmg[i, 0] * pts3D_hmg[i]

    # 使用SVD分解求解最小二乘问题
    _, _, V = np.linalg.svd(A)
    P = V[-1].reshape((3, 4))

    return P

内参与外参计算

内参和旋转比较容易得到，只要对投影矩阵的前面三列进行 RQ 分解即可（注意：RQ 分解和 QR 分解的区别）：

import numpy as np
from scipy.linalg import rq

def get_intrinsic_matrix_and_rot(projection_matrix):
    M = projection_matrix[:, :3]
    K, R = rq(M)
    return K, R

至于位置，就需要进行一些额外的计算：

from scipy.linalg import rq

def get_location(projection_matrix):
    M = projection_matrix[:, :3]
    L = np.sqrt(np.sum(M**2, axis=1)) @ np.array([0.5, 0.5, 0])
    Dm = np.diag([1, 1, L])

    Km, R = rq(Dm @ M)
    E = np.linalg.inv(Km) @ (Dm @ projection_matrix)
    Ic = np.linalg.inv(R) @ E
    return (Ic[0, 3], Ic[1, 3], Ic[2, 3])

MATLAB

MATLAB 在 R2022b 引入了 estimateCameraProjection，文档上写着也是使用 DLT 方法。但 MATLAB 没有内置 RQ 分解。

function [R, Q] = rqdecomp(A)
% RQ decomposition of matrix A
%
% [R,Q]=rqdecomp(A)

[Q, R] = qr(fliplr(A.'), 0);
Q = fliplr(Q).';
R = rot90(R, 2).';
c = sign(diag(R));
c(~c) = 1;
C = spardiag(c);
R = R * C;
Q = C \ Q;
end

function M = spardiag(V)
% makes a sparse n-by-n diagonal matrix with V on the diagonal where V
% is length n.
%
% M=spardiag(V)

if ~isa(V, 'double') || ~islogical(V)
   V = double(V);
end

N = numel(V);
M = spdiags(V(:), 0, N, N);
end