数学中的对称结构与范畴论
对称
对于集合 ,元素 可以是任何东西:
- 线段的两个端点
- 两对坐标
- 两个人
- 两段计算机程序
记第一个元素是 1,第二个元素是 2。存在两种置换:
- 交换:,记为
- 恒等:,记为
在这个基础上,还可以进一步 组合 操作,不难发现,连续交换两次,等于复原,即 。
这样的效果等于恒等置换,即 。于是我们可以说 相当于自己的 逆 置换:。
存在 4 种组合
进一步,可以将这个操作扩展到具有三个端点的三角形。如果记三角形的三个端点为 ,那么有 6 种置换:
- ,恒等置换
这 6 种置换和组合关系称为 。正三角形(等边三角形)在这 6 种置换下都不变,具有最高的 对称性(三条轴对称,绕中心旋转对称) 。
和 不仅可以反映线段、三角形空间的对称,也可以刻画抽象事物的对称。
考虑方程 的两个解 ,根据韦达定理,有:
把 应用上去,我们发现用 交换两个根,方程和韦达定理都仍然成立。加上恒等变换 ,我们发现 可以描述一元二次方程的对称性。
韦达进一步发现,对于三元方程 也有类似的定理。
其中 是方程的三个根。不难发现在 中的 6 种置换下,方程和韦达定理也都成立。 描述了一元三次方程的对称性。
在历史上,正是这种发现孕育出了一个全新的数学分支。数学家们发展出了群来定义、描述、度量对称。并且发现方程可解性的问题,究其本质是方程根的对称性问题。
群
我看出伽罗瓦用来证明这个定理的方法是美妙和完全正确的,在那个瞬间,我体验到了一种强烈的愉悦。—— 法国数学家刘维尔
定义
群 是一个集合 于其定义的某种二元运算 ,它遵循以下四条公理:
- 封闭性公理:对于任何 ,运算结果
- 结合性公理:对于任何 ,有
- 单位元公理: 中存在一个元素 ,使得对任何
- 消去公理:对任何 ,都存在一个逆元 ,使得
一个群的元素个数可以有限也可以无限,分别称为 有限群 和 无限群 。元素的个数叫作这个群的 阶 。
群的「乘法」运算并 不一定满足交换律 。例如所有元素为实数的可逆矩阵与矩阵乘法组成一个群。但 矩阵乘法的顺序是不可交换的 。
如果群中的二元运算满足交换律,则称为 交换群 。为了纪念挪威数学家阿贝尔,人们称交换群为 阿贝尔群 。
幺半群和半群
群的限制条件比较严格,有时我们并不需要一定能够取逆元(例如:整数乘法的逆元并不是整数),如果放宽条件,就可以得到 幺半群 (monoid)这种结构。
幺半群是一个集合 和其上定义的二元运算 ,它们遵循两条公理:
- 结合性公理: 中和任何三个元素满足
- 单位元公理: 中存在一个元素 ,使得对任何
相对于群,去掉了取逆和消去公理。
- 整数乘法构成幺半群,单位元是 1
- 字符串(列表)的连接操作构成幺半群(字符串单位元就是空字符串
"")
1 | class Monoid a where |
如果再进一步把单位元的限制也去掉,我们就得到了 半群 (semigroup)这种代数结构
- 全体正整数构成的加法半群、乘法半群
- 全体偶数构成的加法半群、乘法半群。
1 | instance Semigroup Integer where |
在真实世界里,两个 SQL 语句可以组合成一个新的 SQL 语句;两段 HTML 也可以组合成一个新的 HTML。
群的性质
抽象代数最强大的思想在于我们可以不关心抽象概念所代表的实际物体,而研究抽象结构间内在的规律。这些规律对所有被抽象的物体都适用。
- 群元素代表几何的点、线、面,则我们就获得了几何的规律;
- 群元素是魔方的旋转,我们就获得了魔方变换的规律;
- 群元素是编程中的某种数据结构,我们就得到了这种数据结构上的算法。
- 群的单位元是唯一的。
- 逆元唯一存在。对群中的任意元素 ,都 存在且仅存在一个 使得 。我们称 为 的逆元。
- 有限群的每个元素都有有限的阶。
- 一个集合 的所有一一变换构成一个变换群 。
- 任何一个群都同一个变换群同构。
假设存在从某个集合 到另一个集合 的映射 。 和 是 中的两个元, 和 是它们在 中的像。
考虑 上二元封闭运算产生的元 ,在映射下为 中的像 。如果对 上的二元封闭运算总有:
我们就说 是从 到 的 同态映射(homomorphism)。如果 是满射(surjection,即 中所有元素都在 中有原像),则称为 同态满射 。
举个例子,现在有一个奇数和偶数判定的函数,即 。整数在加法下构成一个群。布尔集合 {True,False} 在逻辑异或 运算下也构成一个群。
- 和 都是奇数, 和 都为
True。它们的和是偶数, 为False。满足 - 和 都是偶数, 和 都为
False。它们的和是偶数, 为False。满足 - 和 是一奇一偶, 和 一个为
True和一个False。它们的和是技术, 为True。满足
如果 不仅是满射,还是 单射 (injection)。那么它就是 一一映射 。这种情况下,我们称 是从 到 的 同构映射 ,简称 同构 (isomorphism)。记为 。另外, 与 之间的同构映射称为 的 自同构 (automorphism)。例如整数加群在取相反数下成为自同构。
如果 和 同构,那么抽象地来看,它们没有什么区别,只有命名上的不同。如果 上有一个代数性质,那么在 上也有一个完全类似的性质。
置换群
和 所在的群家族。伽罗瓦利用它思考方程根的对称性。
一个有限集合的一一变换叫作一个 置换 。一个有限集合的若干个置换做成的一个群叫作一个 置换群(permutation group,它相当于对集合的元素进行重新排列)。
进一步,一个包含 个元素的集合的全体置换做成的群叫作 次对称群(symmetric group)。这个群用 来表示。
基于简单的计数原理, 个元素的排列一共有 个。所以对称群 的阶是
群与对称
记正三角形的三个顶点为 1、2、3,我们取 中的三个元素 (1 2)、(1 2 3) 和 (1 3 2) 对正三角形进行变换:
- 三角形的三个顶点从 123 变为 213,它恰恰是以过点 3 的对称轴进行翻转变换的结果。由于变换前后的图形重合,这说明正三角形是轴对称的。除了 (1 2) 外,它还有另外两个轴对称,分别对应群元素 (1 3)、(2 3)。相应的对称轴是过点 2 和点 1 的高。
- 三角形的三个顶点从 123 变为 231。它等价于绕中心顺时针旋转 120 度。由于变换前后图形重合,这说明正三角形具有 120 度旋转对称性。
- 三角形的三个顶点从 123 变为 312。它等价于绕中心逆时针旋转 120 度,或者顺时针旋转 240 度。由于变换后图形重合,这说明正三角形具有 240 度旋转对称性。
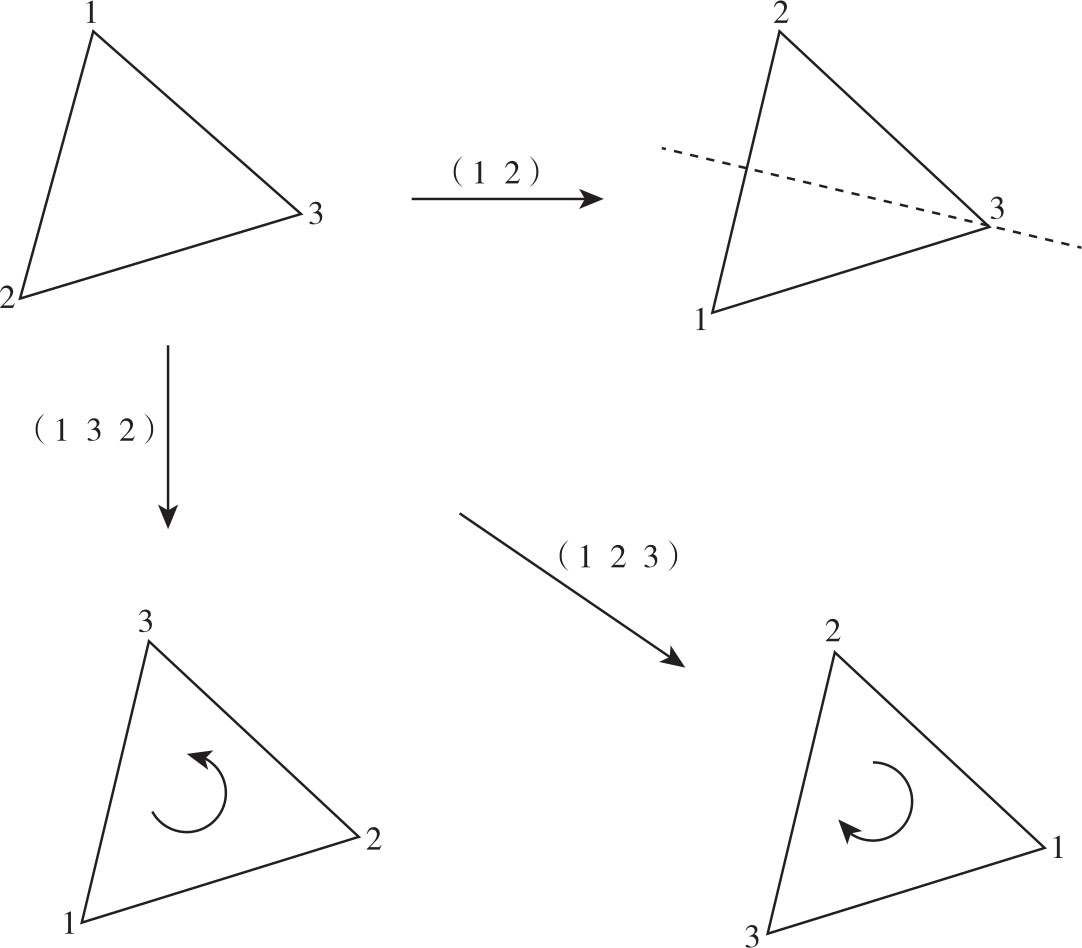
这样正三角形的每种对称性(3 个轴对称、加上 2 个旋转对称性,以及恒等变换)恰好被对称群 的每个元素唯一精确描述了。这就是群与对称间的美妙关系。
我们把这些不改变物体大小的变换称为 叠合 。存在着两种叠合,一种是 真叠合 (proper),另一种是 非真叠合 (improper)。
- 真叠合不改变螺旋的方向(左螺旋仍然是左螺旋,右螺旋仍然是右螺旋)
- 非真叠合改变螺旋的方向(将左螺旋变为右螺旋,右螺旋变为左螺旋)
- 非真叠合又称为 反射
- 它把任一点 P 变成它关于 O 点的对应点 P′:先连接 PO,然后将其延长一倍使得 |PO|=|OP′|。对 O 的反射,通常也称为 反演 。
环与域
现代抽象数学中环和域的概念是由德国女数学家埃米·诺特所发展的。
诺特为爱因斯坦的广义相对论给出了一种纯数学的严格方法,并提出了现代物理学中称为「诺特定理」的观点。诺特善于通过透彻的洞察建立优雅的抽象概念,再将之漂亮地形式化。被帕维尔·亚历山德罗夫、爱因斯坦、迪厄多内、外尔和维纳形容为数学史上最重要的女性。她彻底改变了环、域和代数的理论。在物理学方面,诺特定理解释了对称性和守恒定律之间的根本联系,她还被称为「现代数学之母」。
群是定义了一种运算的系统(集合与乘法运算),而 环 (ring)是定义了 两种运算 的系统。
给定元素 a,b,… 的集合 R,并在之上定义加法 a+b 和乘法 ab,它们的结果也都属于这个集合。其中加法和乘法满足下面的规律。
-
加法的规律
- 结合律:a+(b+c)=(a+b)+c
- 交换律:a+b=b+a
- 存在唯一的单位元,任何元素都有唯一逆元。
-
乘法的规律
- 结合律:a(bc)=(ab)c
-
分配律
- a(b+c)=ab+ac
- (b+c)a=ba+ca
可以看出加法系统构成一个群,并且由于满足交换律,所以是一个阿贝尔加群。而乘法只是封闭的满足结合律的半群。显然,全体整数对于普通加法和乘法构成一个环。另外多项式和矩阵对于加法和乘法也构成一个环。
在环的定义中,我们只要求加法满足交换律,构成阿贝尔群。而对乘法没有要求。如果乘法也满足交换律,我们称这样的环为 交换环 。
在一个交换环里,对于正整数 n 和任何两个元都有:
在环的定义中,我们也 没有要求 环中的乘法一定要有单位元。如果 R 中存在一个元素 e,使得对任何元素都有
则称 为环的单位元。一般来说,一个环未必有单位元。
除环和域
我们知道一个环里不一定所有的元素都有逆元。如果某个环中 所有的非零元素都有逆元 ,就构成一种特殊的环。例如全体有理数对于普通加法和乘法来说显然是一个环,这个环中任意不等于零的元 a 都有逆元。
一个环 R 如果满足以下条件,则叫作 除环 :
- R 至少包含一个不等于零的元;
- R 有一个单位元 1;
- R 的每个不等于零的元都有一个逆元
一个 交换除环 叫作一个 域 。
域是一个可以在其中随意进行加、减、乘、除的数(或者其他东西)系。无论你做多少次四则运算,结果总是同一个域里的数。
按照这一定义,全体有理数构成一个域。同样,全体实数或者全体复数的集合对于普通加法和乘法也各自构成一个域。 和 都不是域,因为两个整数相除未必会得到一个整数。
域比群更常见,因而也更容易理解。群论问题更容易直接应用代数方法解决,域论问题通常是用代数几何方法解决的。
伽罗瓦理论
伽罗瓦理论像是一座桥梁把域和群连接到了一起。域里面有加减乘除四种运算和无穷多个元素,是很复杂的对象。而伽罗瓦理论可以把域中的一些问题 化简到只有一种运算的有限群 里去,整个伽罗瓦理论的核心思想就是这一点。
范畴
如果说,人们将具体的事物,抽象成不带具体意义的数与形是原始阶段;将数、形与计算的意义去除,抽象成代数结构(例如群)和代数关系(例如同构)是第一阶段;范畴可以算是抽象的第二阶段。
范畴论是数学家艾伦伯格和麦克兰恩在 1940 年创立的。
范畴是数学家在 1940 年研究同调代数时的「副产品」——顺手发展出的理论。最近十几年,范畴论由于其强大的抽象,几乎普适于任何问题,正向各种各样的领域渗透。比如各大编程语言纷纷引入 lambda 演算和闭包等结构,有超过 20 种语言已经实现了 单子 (Monad)——用范畴的语言说,叫作「自函子范畴上的幺半群」。许多基本的计算逐渐使用范畴的语言进行抽象。
概述
思考一下食物链,狮子会吃羚羊、羚羊吃草。可以从羚羊画一个箭头指向狮子,从草画一个箭头指向羚羊来表示这样的关系。这样对象加上箭头就构成了一个有结构的,彼此联系在一起的系统。
这样的系统要想成为 范畴 ,还必须满足两点。
- 每个对象都有指向自己的箭头。这种特殊的箭头称为 恒等箭头 。这样每个物种就都有 自指 的箭头了;
- 箭头之间是 可组合的 。草有一个指向羚羊的箭头 ,羚羊有一个指向狮子的箭头 。我们可以把这两个箭头组合起来成为 ,表示草处于狮子食物链的下游。
在组合的基础上,还有一个叫作「可交换」的概念。例如在下图中可以沿着两条通路从草到达狮子,一条是箭头组合 ,表示草在羚羊的下游,羚羊又在狮子的下游;另一条是箭头 ,表示草在狮子的下游。这样我们就相当于得到了一对平行的箭头。
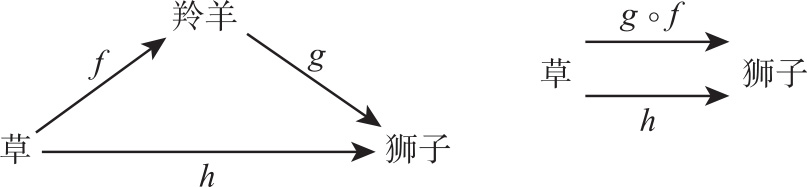
如果这两个平行箭头等效,我们称它们是可交换的。用符号表示为:
这样,我们说草原上的动植物,在食物链关系这个箭头下,构成了一个范畴。现在我们给出较为正式的范畴定义。
定义:一个范畴 包含一组 对象(object)(记为 A,B,C,…)和一组 箭头 (Arrow)(记为 f,g,h,…)。在它们之上定义了以下四种操作:
- 两个全操作,称为源(source)和目标(target),这两个操作都将对象指定到箭头上,记为 ,表示箭头 的源是 A,目标是 B。
- 第三个全操作是 恒等箭头 ,对于任何对象 A,恒等箭头都指向 A 自己。记为 。
- 第四个操作是一个部分操作,称为 组合 。它将两个箭头组合起来。如果有箭头 和 ,则 f 和 g 的组合为 ,读作 「g 然后 f」。它表示 。
除此之外,范畴还必须满足以下两条公理:
- 结合性公理:箭头组合是可结合的。对任何三个可组合的箭头 都有
- 单位元公理:恒等箭头对于组合运算来说相当于单位元。对于任何箭头 来说,都有
范畴的例子
三个幺半群:
- 全体整数中,令 0 是单位元,二元运算是加法,则构成了整数加法幺半群。
- 英文的词语和句子(在编程中称为字符串)构成一个集合,两个英文词句连在一起称为二元运算
- 群元素是字母组成的集合(在编程中称为字符集),二元操作是集合的并,单位元是空集。将两个字母集合并在一起可以获得一个更大的集合。
接下来我们建立这三个幺半群之间的态射(morphism),即转换关系。
首先是从词句幺半群到字母集合幺半群之间的转换关系。
任给一个英文词句,我们可以把这句英文中用到的所有不同字母组成一个集合。可以把这个操作叫作「取字母 」。可以验证,取字母满足以下条件。
以及
也就是说,两句英文字词连在一起所涵盖的字母,等于各个字词中字母的并;空串不含有任何字母(空集)。这是一种很强的转换关系,名叫同态映射。
接下来再定义从字母集合到整数加法幺半群之间的转换关系。任给一个字母集合,我们可以数出它含有多少字母,空集含有 0 个字母。我们把这个操作叫作「数个数 」
和
这样,我们就得到了幺半群范畴 Mon。其中对象是各种各样的幺半群,箭头是彼此间的转换关系,数学上叫作态射。恒等箭头从一个幺半群指向它自己。
函子
函子(functor)就是用来对范畴及其内在的关系(对象和箭头)进行比较的。在某种意义上说,函子好比范畴之间的变换关系(态射)。但是它不仅把一个范畴中的对象映射为另一范畴中的对象,它还将一个范畴中的箭头映射到另一个范畴中。这一点和普通的态射(例如群之间的态射)不同。
函子通常用符号 表示,必须满足两条性质:
- 函子必须保持恒等箭头仍然变换为恒等箭头
- 函子必须能够保持箭头的组合仍然变换为箭头的组合

实际上存在两种变换方式,一种叫做协变,一种叫做反变。
如果一个函子从一个范畴映射到这个范畴本身上,这样的函子被称为 自函子 (endo-functor)。
最简单的函子称为「恒等函子」,它是一个自函子,记为 。它可以作用到任何范畴上,将对象 A 映射为对象 A,将箭头 f 映射为箭头 f。
其次简单的函子叫作「常函子」,它的行为像一个黑洞,我们可以把它记作 。它可以作用到任何范畴上,把所有的对象都映射为黑洞中的对象 B,把所有的箭头都映射为黑洞中的恒等箭头 。黑洞范畴中只有一个恒等箭头,它显然也满足箭头组合的性质:。
2015 年后主流的编程环境都纷纷将 Maybe 概念引入以取代 null 来获取更安全的方法。下图描述了 Maybe 函子的行为:
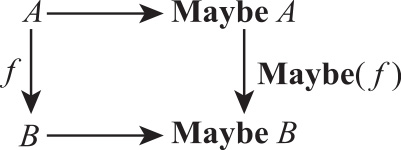
1 | data Maybe A = Nothing | Just A |
参考资料
- 刘新宇. 同构:编程中的数学. 2023
- Will Kurt. Get Programming with Haskell.2018
- 约翰·德比希尔.代数的历史:人类对未知量的不舍追踪(修订版).人民邮电出版社.2021